2090.半径为k的子数组平均值

给你一个下标从 0 开始的数组 nums ，数组中有 n 个整数，另给你一个整数 k 。

半径为 k 的子数组平均值 是指：nums 中一个以下标 i 为 中心 且 半径 为 k 的子数组中所有元素的平均值，即下标在 i - k 和 i + k 范围（含 i - k 和 i + k）内所有元素的平均值。如果在下标 i 前或后不足 k 个元素，那么 半径为 k 的子数组平均值 是 -1 。

构建并返回一个长度为 n 的数组 avgs ，其中 avgs[i] 是以下标 i 为中心的子数组的 半径为 k 的子数组平均值 。

x 个元素的 平均值 是 x 个元素相加之和除以 x ，此时使用截断式 整数除法 ，即需要去掉结果的小数部分。

• 例如，四个元素 2、3、1 和 5 的平均值是 (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75，截断后得到 2 。
  示例 1：

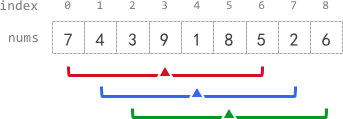
**输入：**nums = [7,4,3,9,1,8,5,2,6], k = 3
输出：[-1,-1,-1,5,4,4,-1,-1,-1]
解释：

• avg[0]、avg[1] 和 avg[2] 是 -1 ，因为在这几个下标前的元素数量都不足 k 个。
• 中心为下标 3 且半径为 3 的子数组的元素总和是：7 + 4 + 3 + 9 + 1 + 8 + 5 = 37 。
  使用截断式 整数除法，avg[3] = 37 / 7 = 5 。
• 中心为下标 4 的子数组，avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4 。
• 中心为下标 5 的子数组，avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4 。
• avg[6]、avg[7] 和 avg[8] 是 -1 ，因为在这几个下标后的元素数量都不足 k 个

1. 入：下标为$i$的元素进入窗口，如果$i<2*k$，重复第一步；
2. 更新，$ans[i-k] = sum / (2*k+1)$ ,$i$对应子数组右端点，而需要将答案记录在中间；
3. 出，下标为$i-2*k$的元素离开窗口。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

class Solution {

public:

    vector<int> getAverages(vector<int>& nums, int k) {

        int n=nums.size();

        vector<int> ans(n,-1);

        long long sum=0;

        for(int i=0;i<nums.size();i++){

            sum += nums[i];

            if(i<2*k) continue;

            ans[i - k] = sum / (k * 2 + 1);

            sum -= nums[i-(2*k)];

        }

        return ans;

    }

};